2.2 Deterministic Finite Automata (DFAs)

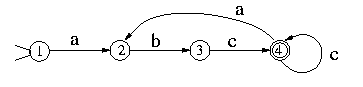
A DFA represents a finite state machine that recognizes a RE. For example, the following DFA:

recognizes (abc⁺)⁺. A finite automaton consists of a finite set of states, a set of transitions (moves), one start state, and a set of final states (accepting states). In addition, a DFA has a unique transition for every state-character combination. For example, the previous figure has 4 states, state 1 is the start state, and state 4 is the only final state.

A DFA accepts a string if starting from the start state and moving from state to state, each time following the arrow that corresponds the current input character, it reaches a final state when the entire input string is consumed. Otherwise, it rejects the string.

The previous figure represents a DFA even though it is not complete (ie, not all state-character transitions have been drawn). The complete DFA is:

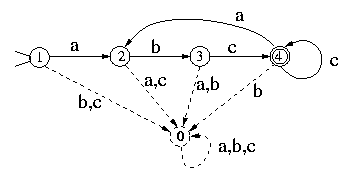
but it is very common to ignore state 0 (called the error state) since it is implied. (The arrows with two or more characters indicate transitions in case of any of these characters.) The error state serves as a black hole, which doesn't let you escape.

A DFA is represented by a transition table T, which gives the next state T[s, c] for a state s and a character c. For example, the T for the DFA above is:

	a	b	c
0	0	0	0
1	2	0	0
2	0	3	0
3	0	0	4
4	2	0	4

Suppose that we want to build a scanner for the REs:

for-keyword	=	for
identifier	=	[a - z][a - z0 - 9]*

The corresponding DFA has 4 final states: one to accept the for-keyword and 3 to accept an identifier:

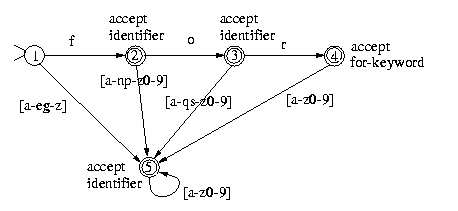
(the error state is omitted again). Notice that for each state and for each character, there is a single transition.

A scanner based on a DFA uses the DFA's transition table as follows:

state = initial_state;
current_character = get_next_character();
while ( true )
{   next_state = T[state,current_character];
    if (next_state == ERROR)
       break;
    state = next_state;
    current_character = get_next_character();
    if ( current_character == EOF )
       break;
};
if ( is_final_state(state) )
   `we have a valid token'
else `report an error'

This program does not explicitly take into account the longest match disambiguation rule since it ends at EOF. The following program is more general since it does not expect EOF at the end of token but still uses the longest match disambiguation rule.

state = initial_state;
final_state = ERROR;
current_character = get_next_character();
while ( true )
{   next_state = T[state,current_character];
    if (next_state == ERROR)
       break;
    state = next_state;
    if ( is_final_state(state) )
       final_state = state;
    current_character = get_next_character();
    if (current_character == EOF)
       break;
};
if ( final_state == ERROR )
   `report an error'
else if ( state != final_state )
   `we have a valid token but we need to backtrack
         (to put characters back into the input stream)'
else `we have a valid token'

Is there any better (more efficient) way to build a scanner out of a DFA? Yes! We can hardwire the state transition table into a program (with lots of gotos). You've learned in your programming language course never to use gotos. But here we are talking about a program generated automatically, which no one needs to look at. The idea is the following. Suppose that you have a transition from state s₁ to s₂ when the current character is c. Then you generate the program:

s1: current_character = get_next_character();
    ...
    if ( current_character == 'c' )
       goto s2;
    ...
s2: current_character = get_next_character();
    ...