lambda-DB: An ODMG-Based Object-Oriented DBMS
One of the key factors for OODB systems to successfully compete with
relational systems as well as to meet the performance requirements of
many non-traditional applications is the development of an effective
query optimizer and a high-performance query evaluation engine. There
are many aspects to the OODB query optimization problem that can
benefit from the already proven relational query-optimization
technology. However many key features of OODB languages present new
and difficult problems not adequately addressed by this
technology. These features include object identity, methods,
encapsulation, subtype hierarchy, user-defined type constructors,
large multimedia objects, multiple collection types, arbitrary nesting
of collections, and nesting of query expressions.
The lambda-DB project at the University of Texas at Arlington aims at
developing frameworks and prototype systems that address the new query
optimization challenges for OODBs. We have already developed a
theoretical framework for query optimization based on an effective
calculus [3]. The system reported here is a fully
operational ODMG 2.0 [2] OODB based on this
framework. Our system can handle most ODL declarations and can process
most OQL queries. lambda-DB is not ODMG compliant. Instead it supports its
own C++ binding that provides a seamless integration between OQL and
C++ with low impedance mismatch. It allows C++ variables to be used
in queries and results of queries to be passed back to C++
programs. To do so, programs expressed in our C++ binding are compiled
by a C++ preprocessor that performs query optimization at
preprocessing time, rather than run-time, as it is proposed by
ODMG. Therefore, all type errors are caught at compile time. The
disadvantage of our approach is that, since optimization is done at
compile time, the execution strategies may become suboptimal at run
time due to updates or, worse, they may even become invalid if indexes
are dropped. The obvious advantage of course is that our system is
very fast. In addition to compiled queries, lambda-DB also supports
execution of ad-hoc OQL queries at run-time by an OQL interpreter.
The lambda-DB system architecture is shown below:
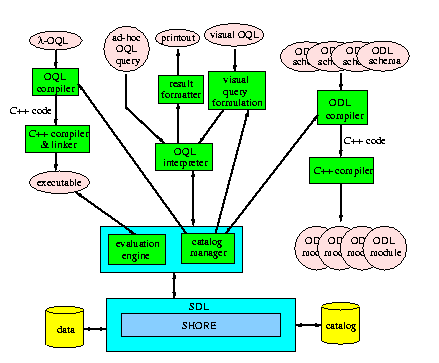
The back-end of our OODB is the SDL (the Shore Data Language) layer of
the SHORE [1] object management system, developed at
the University of Wisconsin. ODL schemas are translated into SDL
schemas in a straightforward way and are stored in the system catalog.
The lambda-DB OQL compiler is basically a C++ preprocessor that accepts a
language called lambda-OQL, which is C++ source code with embedded
DML commands to perform transactions, queries, updates, etc. The
preprocessor generates C++ code that contains calls to the lambda-DB
evaluation engine. This C++ code is compiled and linked to the
appropriate ODL module and it is then executed against the
database. An OQL interpreter is actually a lambda-OQL program and
thus, it has to be linked to ODL modules (because the interpreter may
need to call methods, which are compiled C++ programs). We also
provide a visual query formulation interface, called VOODOO, which
generates OQL text which in turn is interpreted by the OQL
interpreter.
Even though the implementation of our system is simple enough for
other database researchers to use and extend, it is quite
sophisticated since it employs current state-of-the-art query
optimization technologies as well as new advanced experimental
optimization techniques which we have developed through the years, such
as query unnesting. The lambda-DB OODBMS is available as an open source
software through the web at
http://lambda.uta.edu/ldb/doc/.
Query Optimization in lambda-DB
Our OQL optimizer is expressed in a very powerful optimizer
specification language, called OPTL, and is implemented in a flexible
optimization framework, called OPTGEN, which extends our earlier work
on optimizer generators. OPTL is a language for specifying query
optimizers that captures a large portion of the optimizer
specification information in a declarative manner. It extends C++ with
a number of term manipulation constructs and with a rule language for
specifying query transformations. OPTGEN is a C++ preprocessor that
maps OPTL specification into C++ code.
The lambda-DB OQL optimizer proceeds in eight phases: 1) parsing of OQL
queries and translation from OQL into calculus, 2) type checking, 3)
normalization, 4) translation into algebra and query unnesting, 5)
join permutation, 6) physical plan generation, 7) generation of
intermediate evaluation code, and 8) translation from intermediate
code into C++ code, or interpretation of the intermediate code.
Our calculus is called the monoid comprehension
calculus [4]. It captures most features of OQL
and is a good basis for expressing various optimization algorithms
concisely. It is based on monoids, a general template for a data
type, which can capture most collection and aggregate operators
currently in use for relational and object-oriented databases.
One important component of our optimizer is a normalization system for
reducing expressions to a canonical form. Normalization simplifies the
subsequent optimization phases because it reduces the number of forms
to be considered each time. In addition, normalization removes many
forms of query nesting, a process also known as query
decorrelation. All the other forms of query nesting are removed by a
very powerful method [3], which generalizes many
unnesting techniques proposed recently in the literature. In fact, our
system is capable of removing any form of query nesting using a
very simple and efficient algorithm. The simplicity of our method is
due to the use of the monoid comprehension calculus as an intermediate
form for OODB queries. The monoid comprehension calculus treats
operations over multiple collection types, aggregates, and quantifiers
in a similar way, resulting in a uniform way of unnesting queries,
regardless of their type of nesting. Our unnesting algorithm is
compositional, that is, the translation of an embedded query does not
depend on the context in which it is embedded; instead, each subquery
is translated independently, and all translations are composed to form
the final unnested query. Our unnesting algorithm is efficient and
easy to implement (it is only 160 lines of C++ code). In addition to
query unnesting, lambda-DB converts path expressions into pointer joins
between class extents (when is possible) and it uses information about
1:N class relationships to convert unnests into pointer joins between
extents (by using the inverse relationship).
If the comprehension calculus was to be interpreted as is, the
evaluation would proceed in a nested-loop fashion, resembling the
semantics of the calculus, which gives an unacceptable performance for
most non-trivial applications. Research in relational query
optimization has already addressed the related problem of efficiently
evaluating join queries by considering different join orders,
different access paths to data, and different join algorithms. To
effectively adapt this technology to handle our calculus,
comprehensions must be expressed in terms of algebraic operators,
which, eventually, will be mapped into physical execution algorithms,
like those found in relational database systems. This translation is
done in stages: queries in our framework are first translated into
monoid comprehensions, which serve as an intermediate form, and then
are translated into a version of the nested relational algebra that
supports aggregation, quantification, outer-joins, and outer-unnests.
At the end, the algebraic terms are translated into execution plans.
We use both a calculus and an algebra as intermediate forms because
the calculus closely resembles current OODB languages and is easy to
normalize, while the algebra is lower-level and can be directly
translated into the execution algorithms supported by DBMSs.
A very important task of any query optimizer is finding a good order
to evaluate the query operations. In the context of relational
databases, this is known as join ordering. lambda-DB uses a polynomial-time
heuristic algorithm, called GOO, that generates a "good quality"
order of the monoid algebra operators in the query algebraic form.
GOO is a bottom-up greedy algorithm that always performs the most
profitable operations first. The measure of profit is the size of the
intermediate results, but it can be easily modified to use real cost
functions. GOO is based on query graphs and takes into account both
the output sizes of the results constructed in earlier steps and the
predicate selectivities. It generates bushy join trees that have a
very low total size of intermediate results.
After the best evaluation order of operators is derived, the algebraic
form is mapped into an evaluation plan by a rule-based rewriting
system. Our system considers the available access paths (indexes) and
the available physical algorithms to generate different plans. During
this phase, all alternative plans (for the derived order of operators)
are generated and costed and the best plan is selected. Finally, each
evaluation plan is translated into an intermediate evaluation code
that reflects the signatures of the evaluation algorithms used in lambda-DB
(described in the next section). This code can then be
straightforwardly translated into C++ or interpreted by the
lambda-DB interpreter.
The Evaluation Engine
The lambda-DB evaluation engine is built on top of
SHORE [1]. The only layer of SHORE used in our
implementation is SDL (the Shore Data Language) exclusively, because
we believe it is more resilient to changes than the Shore Storage
Manager and is easier to use. An alternative would have been to write
our own value-added server on top of the storage manager. A lot of
effort has been made to make the implementation of the evaluation
engine as simple as possible without sacrificing performance. This
required a very careful design. For example, one of our design
requirements was to put all the evaluation algorithms in a library so
that the query evaluation code would consist of calls to these
algorithms. This sounds obvious enough and simple to implement, but it
required some special techniques (described below) borrowed from the
area of functional programming.
Algebraic operators, such as R |X|_{R.A=S.B} S, are
intrinsically higher-order. That is, they are parameterized by pieces
of code (ie. functions) that specify some of the operation details.
For the previous join, the piece of code is the predicate R.A=S.B.
If it was to be implemented in C++, the join operator could have been
specified as:
Relation join ( Relation x, Relation y, bool (pred) (tuple,tuple) )
where pred is the address of the predicate function. The same
holds for any evaluation plan operator, such as the nested-loop join
operator. If a query is to be compiled into execution code with no
run-time interpretation of predicates, it should make use of
higher-order evaluation algorithms. The alternative (which is adopted
by commercial systems) is to define the evaluation algorithms as kind of
macros to be macroexpanded and individually tailored for each
different instance of the evaluation operator in the query plan. For
example, the nested-loop join would have to be a function with a
`hole' in its body, to be filled with the predicate code. Then the
entire code, the evaluation function and the predicate, is generated
and inserted inside the query code. This is very clumsy and makes the
development and extension of the evaluation algorithms very tedious
and error-prone.
One very important issue to consider when writing evaluation
algorithms is stream-based processing of data (sometimes called
iterator-based processing or pipelining). We would like to avoid
materializing the intermediate data on disk whenever it is
possible. lambda-DB pipelines all evaluation algorithms. Instead of using
threads to implement pipelining, as it is traditionally done in most
systems, we developed a special technique borrowed from the area of
lazy functional languages. Each of our evaluation algorithms is
written in such a way that it returns a piece of data (one tuple) as
soon as it constructs one. To retrieve all the tuples, the algorithm
must be called multiple times. For example, the pipeline version
of the nested-loop join will have the signature:
tuple nested_loop ( Stream sx, Stream sy, bool (pred) (tuple,tuple) )
where Stream is a stream of tuples equipped with standard
operations, such as first and next. In contrast to the
regular nested-loop algorithm, this algorithm exits when it finds the
first qualified tuple (that satisfies pred). To pipeline an
algorithm, we construct a suspended stream, which is a structure
with just one component: an embedded function, which, when invoked, it
calls the evaluation algorithm to construct one tuple. For example, to
pipeline our nested-loop algorithm, we construct a suspended stream
whose embedded function, F, is defined as:
tuple F () { return nested_loop(s1,s2,pred); }
where s1 and s2 are the streams that correspond to the
join inputs and pred is the address of the predicate function.
When a tuple is needed from a suspended stream, its embedded function
is called with no arguments to return the next tuple. This is a clean
and efficient way of implementing pipelining.
This type of evaluation resembles lazy evaluation in
functional programming languages. Here though we provide an explicit
control over the lazy execution, which gives a better handle of
controlling the data materialization on disk.
Currently, the lambda-DB evaluation engine supports table scan of a class
extent, index scan, sorting, block nested-loop join, indexed nested-loop
join, sort-merge join, pointer join, unnesting, nesting (group-by),
and reduction (to evaluate aggregation and quantifications). We are
planning to support hybrid hash join in the
near future.
The intermediate evaluation code, which is generated from a query
evaluation plan, is a purely functional program that consists of calls
to the evaluation algorithms. The functional parameters of the calls
(such as the predicate function of the nested-loop join), are
represented as anonymous functions (lambda abstractions). If the
intermediate code is compiled into C++, the lambda abstractions are
translated into named C++ functions by a simple defunctionalization
process. If the intermediate code is interpreted, each call to an
evaluation algorithm is executed without much overhead because
function addresses are stored into a vector and calls to functions are
dispatched in constant time by retrieving the function directly from
the vector. Lambda abstractions are interpreted by using the address
of the interpreter itself as a parameter and by pushing the body of
the lambda abstraction into a special stack. This form of dispatching
makes the interpreter very compact (it is 400 lines of C++ code only)
and very fast.
[1] M. Carey et al. Shoring Up Persistent Applications. In SIGMOD'94, pp 383-394.
[2] R. Cattell et al. The Object Database Standard: ODMG 2.0. Morgan Kaufmann, 1997.
[3] L. Fegaras. Query Unnesting in Object-Oriented Databases. In SIGMOD'98, pp 49-60.
[4] L. Fegaras and D. Maier. Towards an Effective Calculus for Object Query Languages. In SIGMOD'95, pp 47-58.
Last modified: 1/8/00 by Leonidas Fegaras
